Question

I need to know the following steps to find the range and domain.

Answer 1

`f(x)=\sqrt[]{x^2+1}`

In a radical function as given the domain is any x-value for which the radical (value under the radical sing) is not negative:

`\begin{gathered} x^2+1\ge0 \\ x^2\ge-1 \\ \end{gathered}`

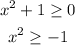
As any value of x makes x squared be possitive or 0, the domain is:

`\begin{gathered} x\in\R \\ Interval\text{ notation:} \\ (-\infty,\infty) \end{gathered}`

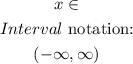
Any value of x makes x squared greater than or equal to zero the range is:

`\begin{gathered} x^2\ge0 \\ \\ \text{Range stars in x=0:} \\ f(0)=\sqrt[]{0+1} \\ f(0)=\sqrt[]{1} \\ f(0)=1 \\ \\ Range\colon \\ y\ge1 \\ \\ \text{Interval notation;} \\ \lbrack1,\infty) \end{gathered}`