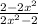
Step1
we can factor the numerator and denominator because we have a square subtract
![\begin{gathered} \frac{(\sqrt[]{2}+\sqrt[]{2}x)(\sqrt[]{2}-\sqrt[]{2}x)}{(\sqrt[]{2}x-\sqrt[]{2})(\sqrt[]{2}x+\sqrt[]{2})} \\ \\ \frac{(\sqrt[]{2}+\sqrt[]{2}x)}{\sqrt[]{2}x+\sqrt[]{2})}\cdot\frac{(\sqrt[]{2}-\sqrt[]{2}x)}{(\sqrt[]{2}x-\sqrt[]{2})} \\ \\ 1\cdot-1 \\ \\ =-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/z2zczvvahbbq0h9o9tt51t7xxqa5fo2e85.png)
step 2
restricted values of X are when the denominator is 0
then
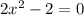
factor this
![(\sqrt[]{2}x-\sqrt[]{2})(\sqrt[]{2}x+\sqrt[]{2})=0](https://img.qammunity.org/2023/formulas/mathematics/college/x0yqrymol31bvf1yviwb2dcg5yzuxia7hc.png)
and find the value of x what make each parenthesis 0
![\begin{gathered} \sqrt[]{2}x-\sqrt[]{2}=0 \\ \sqrt[]{2}x=\sqrt[]{2} \\ x=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1axx9xmfojna5ohu4t5imcpb08y4ofp36k.png)
first restricted value is x=1
![\begin{gathered} \sqrt[]{2}x+\sqrt[]{2}=0 \\ \sqrt[]{2}x=-\sqrt[]{2} \\ x=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8q7s3zl28yag4600xsnkqawxii90z763bf.png)
and the other restricted value is x=-1