Question

WXYZ is a quadrilateral graphed in the coordinate plane with vertices W(0,5),X(-3,2), Y(0,-4), and Z(3,2). What are the lengths of the sides of the quadrilateral, and what is the correct name for the figure?

Answer 1

Given: WXYZ is a quadrilateral graphed in the coordinate plane with vertices W(0,5), X(-3,2), Y(0,-4), and Z(3,2).

Required: To determine the side length and type of quadrilateral.

Explanation: The distance between two points is given by the formula-

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

The length of side WX is-

`D=√((-3-0)^2+(2-5)^2)`

Further solving as-

`\begin{gathered} D=√(9+9) \\ D=3√(2)\text{ units} \\ D=4.24\text{ units} \end{gathered}`

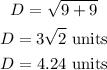
Similarly, the side length XY is-

`\begin{gathered} D=√((0+3)^2+(-4-2)^2) \\ D=√(45) \\ D=6.71\text{ units} \end{gathered}`

And, the side length YZ is-

`\begin{gathered} D=√((3-0)^2+(2+4)^2) \\ D=√(45) \\ D=6.71\text{ units} \end{gathered}`

Finally, the side length WZ is-

`\begin{gathered} D=√((3-0)^2+(2-5)^2) \\ D=3√(2) \\ D=4.24\text{ units} \end{gathered}`

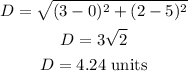
Now, since the adjacent sides of the quadrilateral WXYZ are equal, the quadrilateral is a Kite.

Final Answer:

The length of side WX=4.24 units.

The length of side XY=6.71 units.

The length of side YZ=6.71 units.

The length of side ZW=4.24 units.

The best name for this quadrilateral is Kite.