Question

7. Brian is packing boxes that can contain two types of items, board games and remote control cars. Board games weigh 3 pounds and remote controlled cars weigh 1.5 pounds, and the box can hold no more than 24 pounds. Also, in each box, the amount of remote control cars must be at least 4 times the amount of board games. Let x represent the number of board games. Let y represent the number of remote controlled cars.A. Write the system of inequalities that represents this situation. You should have 2 different inequalities that you wrote. B. Graph the system of inequalities on the coordinate plane below.

Answer 1

A)

`\begin{gathered} 3x+1.5y\leq24\Rightarrow inequality(1) \\ y\ge4x\rightarrow inequality(2) \end{gathered}`

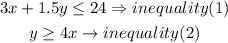
Step-by-step explanation

Step 1

Let x represents the number of board games

Let y represent the number of remote controlled cars

i)

a)Board games weigh 3 pounds

b) remote-controlled cars weigh 1.5 pounds

The box can hold no more than 24 pounds( in other words it must be equal or less thant 24),so

`3x+1.5y\leq24\Rightarrow inequality(1)`

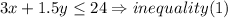
ii) in each box, the amount of remote control cars must be at least 4 times the amount of board games( in other words, the number of remote control cars must be equal or greater than 4 times the amount of board games, so,

hence

`y\ge4x\rightarrow inequality(2)`

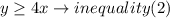
so,

A)

`\begin{gathered} 3x+1.5y\leq24\Rightarrow inequality(1) \\ y\ge4x\rightarrow inequality(2) \end{gathered}`

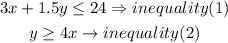
Step 2

graph the inequalities

a) set the sign = to convert the inequality in a funcion, isolate for y

b) fnd 2 coordinates of the line

C) draw the line

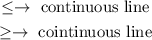
`\begin{gathered} \leq\rightarrow\text{ continuous line} \\ \ge\rightarrow\text{ cointinuous line} \end{gathered}`

i)

`\begin{gathered} 3x+1.5y=24 \\ 1.5y=24-3x \\ y\leq(24-3x)/(1.5) \\ y=16-2x \\ \text{when x= 0} \\ y=16-0 \\ so,P1(0,16) \\ \text{when =3} \\ y=16-2(3) \\ y=16-6=10 \\ so\text{, P2(3,10)} \end{gathered}`

draw a line(continuosus) that passes trougth P1 and P2

ii)

`\begin{gathered} y\ge4x\rightarrow y=4x \\ \text{when x=0} \\ y=4\cdot0=0 \\ so\text{ , P3(}0,0) \\ \text{and when x= 2} \\ y=4(2)=8 \\ so,\text{ P4}(2,8) \end{gathered}`

draw a line(continuosus) that passes trougth P3 and P4

I hope this helps you