Problem Statement
The question asks us to plot the function:
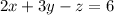
And we were asked to state the x-, y- and z- intercepts.
Solution
The equation given is a 3-d equation as such when it is plotted, it gives a plane instead of a line for a normal linear 2-D equation.
We shall begin with the intercepts. To find the intercepts, we simply set x, y to zero to find the z-intercept, x, z to zero to find the y-intercept, and y, z to zero to find the x-intercept.
Let us proceed to find the intercepts:

The intercepts are:
x-intercept = 3
y-intercept = 2
z-intercept = -6
Graphically, we can observe these intercepts shown below:
The above figure shows the x and z intercepts.
The y-intercept is shown below:
The final image of the plane will look like this: