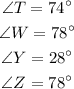We have the next two triangles
And we must find the missing angles.
Since they are similar triangles we know that their angles are congruent. That means,
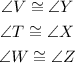
Using that,
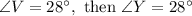
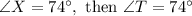
Now, to find the las angle of each triangle we must use that the interior angles of a triangl add up to 180°
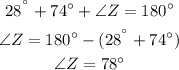
Finally,
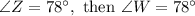
ANSWER: