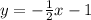Question

Find the equation that is perpendicular to the equation that’s given

Answer 1

Given: The equation below

`\begin{gathered} y=2x+4 \\ Point:(2,-2) \end{gathered}`

To Determine: The equation that is perpendicular to the given equation

Solution

The given equation can be represented using the slope-intercept form

`\begin{gathered} slope-intercept-form:y=mx+c \\ Where \\ m=slope \\ c=intercept \end{gathered}`

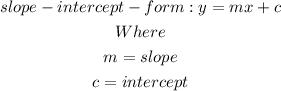
Let us determine the slope of the equation

`\begin{gathered} y=mx+c \\ y=2x+4 \\ m=2,c=4 \end{gathered}`

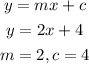
Therefore, the slope is 2

Please note two linear equations are perpedicular if the slope one is a negative inverse of the other

So, we have

`\begin{gathered} m_1=-(1)/(m) \\ m_1=slope\text{ of the perpendicular equation} \end{gathered}`

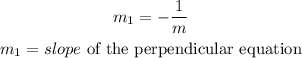
Given the slope and a point, we can determine the equation using the formula below

`\begin{gathered} point(x_1,y_1),slope(m) \\ (y-y_1)/(x-x_1)=m \end{gathered}`

Let us substitute the slope and the coordinate of the points given

`\begin{gathered} (y--2)/(x-2)=-(1)/(2) \\ (y+2)/(x-2)=-(1)/(2) \\ y+2=-(1)/(2)(x-2) \\ y+2=-(1)/(2)x+1 \\ y=-(1)/(2)x+1-2 \\ y=-(1)/(2)x-1 \end{gathered}`

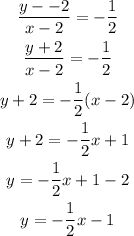
Hence, the equation of the perpendicular to the given equation is

`y=-(1)/(2)x-1`