To find the length of AC, we must form a proportional relation between the triangles. Observe that EF corresponds to BC, and DE corresponds to AB.
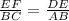
Replacing all the given expressions, we have.
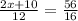
Now, we solve for x.
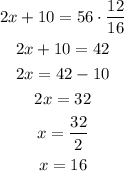
Then, we use this value to find AC.
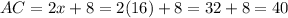
Therefore, AC must be 40 units long to prove that the triangles are similar.