Answer:
2.333 m/s to the right
Step-by-step explanation:
By the conservation of momentum, we can write the following equation:
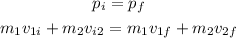
Where m1 and m2 are the masses of the balls, vi, and vf are the initial and final velocities. If we take to the right as a positive and to the left as negative, we get
m1 = 2 kg
v1i = 3 m/s
m2 = 3 kg
v2i = -1 m/s
v1f = - 2 m/s
v2f = ?
Replacing the values and solving for v2f, we get:
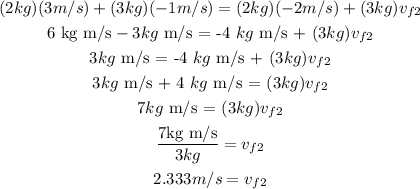
Therefore, the velocity of the 3 kg ball is 2.333 m/s to the right.