Given:
The radius of a cylinder = r
And the height of the cylinder = h
The radius of the cylinder is multiplied by 8 while the height is kept the same.
We will find the volume of the original and new cylinders
The volume of the original cylinder will be:

The volume of the new cylinder will be:
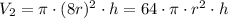
Compare the two volumes:
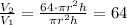
So, when the radius of the cylinder is multiplied by 8 while the height is kept the volume will be 64 times the original cylinder.