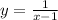Question

2. Write an equation for a function that is discontinous at x = 1:a) with a holeb) with a jump discontinuityc) with a vertical asymptote

Answer 1

For this problem, we need to write the equation to a function that has a discontinuity at x = 1.

First, we need to find one that has a hole at x = 1. This is shown below:

`y=((x+2)(x-1))/((x-1))`

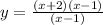
This function is not defined at the point x = 1, therefore it will have a whole on that point.

Then we need to find a jump discontinuity, meaning that the function will abruptly change from one value to the other on that point. We have:

`y=\begin{cases}x+2,\text{ for }x<1{} \\ x^2,\text{ for }x\geqslant{1}\end{cases}`

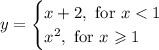
We need to determine a function with a vertical asymptote in 1. For that, we need to use a rational function with a denominator equal to "x-1".

`y=(1)/(x-1)`