Question

A rocket burns at the rate of 2 tons/min after falling out of orbit into the atmosphere. If a rocket weighted 5300 tons before reentry, express its weight w as a function of the time t, in minutes, of reentry. Write the weight of the rocket as the function w(f)(Simplify) Do not factor

Answer 1

The weight of the rocket before entry is

`=5300`

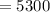
The rate of the rocket burn given is

`=2\text{ tons/min}`

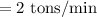
Let the time for the burnout be represented as

`=t`

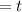
The weight of the rocket to be burnt out will be calculated using the formula below

`\begin{gathered} w=\text{rate}* time \\ w=2* t \\ w=2t \end{gathered}`

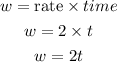
Burn out means the weight of the rocket is reducing so there will be a negative value

`=-2t`

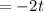
Hence,

The equation of the weight as a function of t will be

`w(t)=-2t+5300`

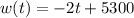
Hence,

The final answer is w(t) = -2t + 5300