Question

A box of mass 8 kg is moving at 9 m/s and collides with a 16 kg stationaryball.After the collision, the box continues in the same direction with avelocity of 3 m/s. Neglecting friction, the velocity of the ball after them/s. *collision is -

Answer 1

According to law of conservation of momentum we have,

`m_1v_(1i)+m_2v_(2i)=m_1v_(1f)+m_2v_(2f)_{}_{}`

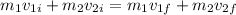
Where,

Substituting these values in the above equation,

`8*9+16*0=8*3+16* v_(2f)`
`v_(2f)`

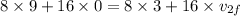
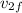
V2f is what we need to find out

Simplifying the above equation,

`72=24+16* v_(2f)`

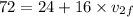
which implies

`v_(2f)=(72-24)/(16)=(48)/(16)`

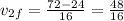
Which gives us

`v_(2f)=3`

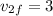
i.e. The velocity of the ball after the collision is 3 m/s