Question

I don’t know the first part of this question but Ik the 2nd part so what’s the answer to the first one?

Answer 1

The free-body diagram of the given problem is the following:

In the diagram we have the following forces:

`\begin{gathered} T=\text{ tension} \\ T_y=y-component\text{ of the tension} \\ T_x=\text{horizontal component of the tension} \\ mg=\text{ weight} \\ m=\text{ mass} \\ g=\text{ acceleration of gravity} \\ T_H=\text{horizontal tension} \end{gathered}`

We are asked to determine the tension in the horizontal tension we will add the horizontal forces:

`\Sigma F_h=T_x-T_H`

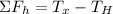
Since there is no movement in this direction this means that the sum of forces must be equal to zero, therefore, we have:

`T_x-T_H=0`

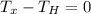
Solving for the horizontal tension we get:

`T_H=T_x`

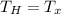
From the following right triangle we can determine the value of the x-coordinate of the tension "T":

We can use the function cosine and we get:

`\cos 37=(T_x)/(T)`

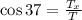
Now we multiply both sides by T:

`T\cos 37=T_x`

Now we substitute this value in the sum of forces:

`T_H=T\cos 37`

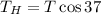
Now we need to determine the value of "T". To do that we will add the vertical forces, we get:

`\Sigma F_v=T_y-mg`

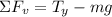
Since there is no vertical movement the forces add up to zero, we get:

`T_y-mg=0`

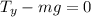
Now we use the same right triangle to get the value of the y-component of the tension:

`\sin 37=(T_y)/(T)`

Multiplying both sides by "T":

`T\sin 37=T_y`

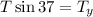
Now we substitute in the sum of vertical forces:

`T\sin 37-mg=0`

Now we solve for "T", first by adding "mg" to both sides:

`T\sin 37=mg`

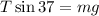
Now we divide both sides by "sin37":

`T=(mg)/(\sin37)`

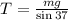
Now we substitute this value in the formula for the horizontal tension:

`T_H=(mg)/(\sin37)\cos 37`

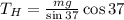
Now we substitute the values:

Now we solve the operations:

`T_H=949.37N`

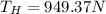
Therefore, the tension in the horizontal section is 949.37N.