Find the exact value of sin G.A. √1010B. 3√1010C. 4√10D. 160

Question

asked May 5, 2023 132k views

1 Answer

Tom Swirly · Answer 1 · 2023-05-11T03:14:10+0000

Given the Right Triangle EFG, you know that:

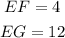
$\begin{gathered} EF=4 \\ EG=12 \end{gathered}$

By definition:

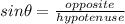
$sin\theta=(opposite)/(hypotenuse)$

Since, in this case:

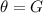
$\theta=G$

You can identify that:

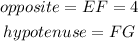
$\begin{gathered} opposite=EF=4 \\ hypotenuse=FG \end{gathered}$

In order to find the hypotenuse of the Right Triangle, you need to use the Pythagorean Theorem, which states that:

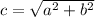
Where "c" is the hypotenuse, and "a" and "b" are the legs of the Right Triangle.

You can set up that:

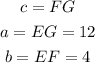
$\begin{gathered} c=FG \\ a=EG=12 \\ b=EF=4 \end{gathered}$

Therefore:

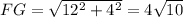
Now you can determine that:

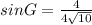
Simplify:

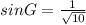
You can multiply the numerator and the denominator by:

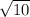
In order to Rationalize the denominator:

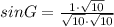
$sinG=(1\cdot√(10))/(√(10)\cdot√(10))$
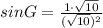
$sinG=(1\cdot√(10))/((√(10))^2)$
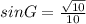
sinG=(√(10))/(10)

Hence, the answer is: Option A.