Question

Margaret needs to put a new gutter on one side of her roof. The shape of her roof is made up of two right triangles that are on each side of a square. If the area of the square is 2500ft2 and the base of each of the triangles is 85ft, what is the total length of the gutter she’ll need to replace?

Answer 1

Given:

The area of square = 2500 ft²

The base of each triangle = 85 ft

Required:

Total length of the gutter she will need to replace

Step-by-step explanation:

To find the length of the square we need to apply the formula of area of square

`area\text{ }of\text{ }square=side^2`

Substituting the value of area of square in the above formula we get

`\begin{gathered} area\text{ }of\text{ }square=side^2 \\ \\ 2500=side^2 \\ \\ side=√(2500) \\ \\ side=50\text{ }ft \end{gathered}`

So the length of the side of the square is 50ft.

It means that the height of each triangle is 50ft. Since the triangles are right angled triangle we can find the length of the hypotenuse by applying the pythagoras theorem, which is given as

`hypotenuse^2=base^2+height^2`

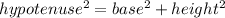
Substituting the value of base and height we can find the value of hypotenuse

`\begin{gathered} hypotenuse^2=85^2+50^2 \\ \\ hypotenuse^2=7225+2500 \\ \\ hypotenuse^2=9725 \\ \\ hypotenuse=√(9725)=98.61ft \end{gathered}`

The total length of the gutter would be the sum of the sides of the square and the two triangles

`\begin{gathered} total\text{ }length=98.61+98.61+85+85+50+50 \\ \\ total\text{ }length=467.22ft \end{gathered}`

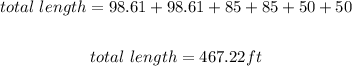
Final Answer:

The total length of the gutter Margaret would need to replace is 467.22 ft.