Question

My main question is how to solve for the a and the p and which way it opens i also dont understand how to find the directrix

Answer 1

First, let's understand how it opens. A parabola equation have one of the following forms

`y=a(x-h)^2+k`

Or

`x=a(y-h)^2+k`

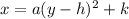
Both are written in vertex form. If we have the first equation, the parabola opens upward(if a > 0) or downward(if a < 0), if we have the second equation it opens to the left(if a < 0) or to the right(if a > 0).

Our equation is

`y=(1)/(4)(x+2)^2-4`

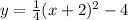
Comparing to our equations written in standard form, we have the first equation with a positive a, therefore, this parabola opens upward.