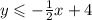Question

2) Explain the steps on how you would write x + 2y < 8 in slope intercept form.

Answer 1

`y\leqslant-(1)/(2)x+4`

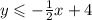
Step-by-step explanation

The slope-intercept form of a line is,

`y=mx+b`

In this case, we have an inequality but the steps to rewrite it in the slope-intercept form are similar to the ones we would use if we had an equality.

Step 1: subtract x from both sides of the inequality,

`\begin{gathered} x-x+2y\le8-x \\ \\ 2y\le-x+8 \end{gathered}`

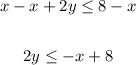
Step 2: divide both sides by 2,

`\begin{gathered} (2y)/(2)\le(-x+8)/(2) \\ \\ y\le(-x+8)/(2) \end{gathered}`

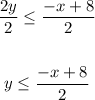
Step 3: distribute the denominator and simplify the fractions if possible,

`\begin{gathered} y\le(-x)/(2)+(8)/(2) \\ \\ y\le-(1)/(2)x+4 \end{gathered}`

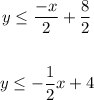
Hence, the inequality in slope-intercept form is,

`y\leqslant-(1)/(2)x+4`