hello
to solve this question, we can write out two sets of equation and solve them
let the short answers be represented by x
let the multiple-choice questions be represented by y
we know that the test has 60 points
multiple-choice carries 2 points
short answers carries 5 points
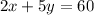
now we have a total of 15 questions which comprises of multiple-choice questions and short answers
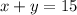
now we have two set of equations which are
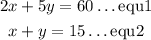
now let's solve for x and y
from equation 2, let's make x the subject of formula
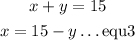
put equation 3 into equation 1

now we know the value of y which is the number of multiple-choice question. we can use this information to find the number of short answer through either equation 1 or 2
from equation 2
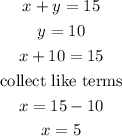
from the calculations above, the number of short answers is equal to 5 and multiple-choice questions is equal to 10.
The answer to this question is option C