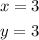Question

Can someone please help me solve and help me graph for this equation?

Answer 1

Graph both equations. The coorinates of the point where the graphs intersect is the solution to the system of equations.

To graph them, notice that each equation corresponds to a line. A straight line can be drawn if two points on that line are given. Replace two different values of x into each equation to find its corresponding value of y, then, plot the coordinate pairs (x,y) to draw the lines.

First equation:

`y=2x-3`

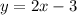
For x=2 and x=5 we have that:

`\begin{gathered} x=2 \\ \Rightarrow y=2(2)-3 \\ =4-3 \\ =1 \end{gathered}`
`\begin{gathered} x=5 \\ \Rightarrow y=2(5)-3 \\ =10-3 \\ =7 \end{gathered}`

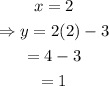
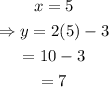
Then, the points (2,1) and (5,7) belong to the line:

Second equation:

`x+3y=12`

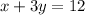
For x=0 and x=6 we have:

`\begin{gathered} x=0 \\ \Rightarrow0+3y=12 \\ \Rightarrow3y=12 \\ \Rightarrow y=(12)/(3) \\ \Rightarrow y=4 \end{gathered}`
`\begin{gathered} x=6 \\ \Rightarrow6+3y=12 \\ \Rightarrow3y=12-6 \\ \Rightarrow3y=6 \\ \Rightarrow y=(6)/(3) \\ \Rightarrow y=2 \end{gathered}`

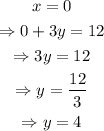
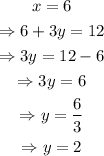
Then, the points (0,4) and (6,2) belong to the line:

Solution:

The lines intersect at the point (3,3).

Then, the solution for this system of equations, is:

`\begin{gathered} x=3 \\ y=3 \end{gathered}`