Question

How do I set this up and how do I know what am I looking for

Answer 1

We have to calculate the number of seconds for the flare to return to the sea.

We have an initial vertical speed of 448 ft/s.

The only force acting on the flare is gravity.

Then, we can model the heigth in function of time using the equation:

`h(t)=h_0+v_yt-(g)/(2)t^2`

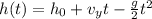
where h0 = 0 ft, vy = 448 ft/s and g = 32 ft/s².

Then, we can replace and calculate t for h(t) = 0, that is the time it took the flare to come back to the initial height (that is 0 ft):

`\begin{gathered} h(t)=0 \\ h_0+v_yt-(g)/(2)t^2=0 \\ 0+448t-(32)/(2)t^2=0 \\ 448t=16t^2 \\ 448=16t \\ t=(448)/(16) \\ t=28 \end{gathered}`

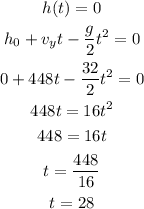
Answer: it will take 28 seconds for the flare to return to the sea [Third option].