Question

Find the length and width of a rectangle sandbox, where the length is 3 feet longer than it’s width if you are building it with 22 feet of lumber

Answer 1

Let the length be represented by l and the width, w.

The question says that the length is 3 feet longer than the width. This means that

`l=w+3`

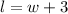
The perimeter of a rectangle is given as

`2(w+l)=P`

The perimeter of the sandbox is given as 22 feet.

Substituting the values for the perimeter and the length (w + 3) into the perimeter formula, we have

`2(w+w+3)=22`

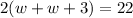
Solving, we have

`\begin{gathered} 2(2w+3)=22 \\ 2w+3=(22)/(2) \\ 2w=11-3 \\ 2w=8 \\ w=(8)/(2) \\ w=4 \end{gathered}`

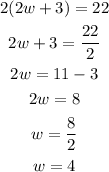
Now that we have the value for the width, we can calculate the length as

`\begin{gathered} l=w+3 \\ l=4+3 \\ l=7 \end{gathered}`

The length is 7 feet and the width is 4 feet.