Question

What is the slope intercept form of (3,1) and (9,-7)

Answer 1

The slope-intercept form of a line is given by:

`y=mx+b`

Where

• m is the slope of the line.

,

• b is the y-intercept of the line. At this point, x = 0.

Since we have two points: (3, 1) and (9, -7), we can use the two-points form of the line equation as follows:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

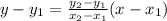
Now, we can label both points as follows:

• (3, 1) ---> x1 = 3, y1 = 1

,

• (9, -7) ---> x2 = 9, y2 = -7

If we apply the two-points form of the line equation, we have:

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-1=(-7-1)/(9-3)(x-3) \\ y-1=(-8)/(6)(x-3) \\ y-1=-(4)/(3)(x-3) \\ y-1=(-(4)/(3))(x)+(-(4)/(3))(-3) \\ y-1=-(4)/(3)x+4(-(3)/(-3)) \\ y-1=-(4)/(3)x+4(1) \\ y-1=-(4)/(3)x+4 \end{gathered}`

If we add 1 to both sides of the equation, we finally have:

`\begin{gathered} y-1+1=-(4)/(3)x+4+1 \\ y=-(4)/(3)x+5 \end{gathered}`

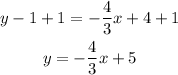
In summary, therefore, the slope-intercept form of the line that passes through the points (3, 1) and (9, -7) is:

`y=-(4)/(3)x+5`