Question

1. The vertical asymptote is x=3. 2. The vertical asymptote is x=-4. 3. The x-intercepts is (4,0). 4. The y-intercepts is (0,-3).

Answer 1

the vertical asymptote is x = -4 (option 2)

Step-by-step explanation:
`f(x)\text{ =}(x-3)/(x+4)`

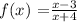
The vertcal asymptote of a function, is the value of x when the denominator is equated to zero:

`\begin{gathered} \text{Denominator = x + 4} \\ \text{equating to zero:} \\ x\text{ + 4 = 0} \\ \text{subtract 4 from both sides:} \\ x\text{ +4 -4 = 0 - 4} \\ x\text{ = -4} \end{gathered}`

The x - intercept is the value of x when f(x) = 0

`\begin{gathered} f(x)\text{ =}(x-3)/(x+4) \\ 0\text{ = =}(x-3)/(x+4) \\ 0(x\text{ + 4) = x - 3} \\ 0\text{ = x - 3} \\ x\text{ = 3} \\ x-\text{intercept: }(3,\text{ 0)} \end{gathered}`

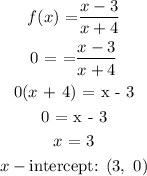
The y-intercept is the value of f(x) when x = 0

`\begin{gathered} f(x)\text{ = }(x-3)/(x+4) \\ f(x)\text{ =}(0-3)/(0+4) \\ f(x)\text{ = }=\text{ }(-3)/(4) \\ y-\text{intercept = (0, -3/4)} \end{gathered}`

Comparing the results we got and the options, the only option that has same answer as our calculation is the vertical asymptote is x = -4 (option 2)