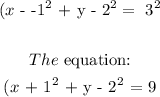Answer:
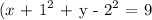
Step-by-step explanation:
Given:
A circle on a coordinate plane with a dot representing the center
To find:
Equation of the circle
The formula for the equation of a circle is given as:
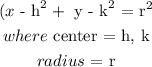
Identifying the coordinate of the center and the unit for the radius:
Center (h, k) = (-1, 2)
h = -1, k = 2
radius = 3 units from the center to the circumference
r = 3
substitute the values into the formula: