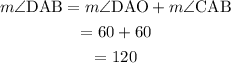Answer:
• mAD=60°
,
• mBF=60°
,
• mCF=60°
,
• m∠COD=120°
,
• m∠B=90°
,
• m∠C=30°
,
• m∠D=60°
,
• m∠DAB=120°
Step-by-step explanation:
The line AC is the diameter of the circle.
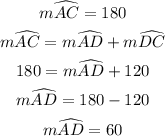
Similarly, line DF is a diameter, thus:
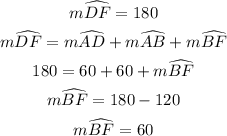
In like manner, using line DF:
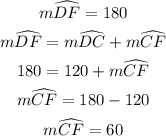
Angle COD is the central angle subtended by arc CD at the centre.
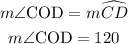
Angle B is the angle subtended by the diameter AC at the circumference of the circle. The angle in a semicircle is 90 degrees, therefore:
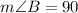
Angle C is the angle subtended by arc AB at the circumference.
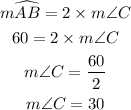
Next, we find the measure of angle D.
In Triangle AOD,
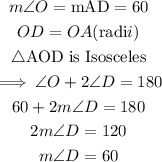
Finally, we find the measure of angle DAB.