Question

Find the area to the nearest square foot of the shaded region below, consisting of a square with a circle cut out of it. Use as an approximation for .

Answer 1

The image shows a square with a circle cut out of it.

We need to compute the area of the square and subtract the area of the circle to find the shaded area.

The area of a square of side length x is:

`A_s=x^2`

We are given the side length of x = 10 ft, thus:

`A_s=(10ft)^2=100ft^2`

The area of a circle of radius r is given by:

`A_c=\pi r^2`

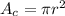
The circle inside the square has a diameter of d=10 ft, thus its radius is r = 10/2 = 5 ft. Calculating the area:

`A_c=\pi(5ft)^2=25\pi ft^2`

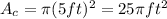
Using π=3.14:

`A_c=25\cdot3.14ft^2=78.5ft^2`

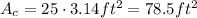
Now, subtracting areas:

`A_{\text{shaded}}=100ft^2-78.5ft^2=21.5ft^2`

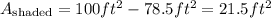
Rounding to the next integer, the required area is approximately 22 square ft

Choice: 22 square ft