Question

A 4.80-kg block is at rest on a horizontal floor. If you push horizontally on the 4.80-kg block with a force of 12.0 N, it just starts to move.What is the coefficient of static friction?

Answer 1

The given problem can be exemplified using the following free-body diagram:

In the diagram we have:

`\begin{gathered} N=\text{ normal force} \\ m=\text{ mass} \\ g=\text{ acceleration of gravity} \\ F=\text{ pushing force} \\ F_f=\text{ friction force} \end{gathered}`

Now, we are asked to determine the coefficient of static friction. To do that we will add the forces in the horizontal direction. We will take the forces to the left as positive, we get:

`\Sigma F_h=F-F_f`

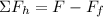
Now, since we are considering the moment that the object will begin its movement we will use an acceleration of zero, therefore, the sum of forces is equal to zero:

`F-F_f=0`

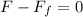
Now, To determine the value of the force of friction we will use the following relationship:

`F_f=\mu_sN`

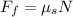
Where:

`\mu_s=\text{ coefficient of static friction}`

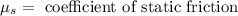
Now, we determine the normal force by adding the forces in the vertical direction, we get:

`\Sigma F_v=N-mg`

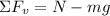
Since there is no movement in this direction the sum of forces must be equal to zero:

`N-mg=0`

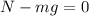
Now we solve for the normal force by adding "mg" to both sides:

`N=mg`

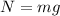
Now we substitute this value in the formula for friction:

`F_f=\mu_smg`

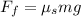
Now we substitute in the sum of horizontal forces:

`F-\mu_smg=0`

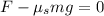
Now we will solve for the coefficient of static friction, to do that we will add the relationship for the friction on both sides:

`F=\mu_smg`

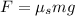
Now we divide both sides by "mg":

`(F)/(mg)=\mu_s`

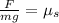
Now we substitute the values:

Solving the operations we get:

`0.26=\mu_s`

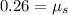
Therefore, the coefficient of static friction is 0.26.