Question

the enrollment at a new school increases at a constant percent rate. after y years , the number of students enrolled is given by the expression 52 • 3 y/5

Answer 1

After y years the number of students is given as,

`52\cdot3^{(y)/(5)}`

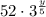
The number of students when school has opened can be determined as,

`52\cdot3^{(0)/(5)}=52`

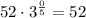
Thus, the number of students when the school has opend is 52.

The number of years after which the number of students triple can be determined as,

`\begin{gathered} 52\cdot3^{(y)/(5)}=52*3 \\ 3^{(y)/(5)}=3 \\ (y)/(5)=1 \\ y=5 \end{gathered}`

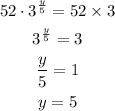
Thus, required value of number of years is 5.

The factor by which the number of enrollment increases from one year to another can be determined as,

`\begin{gathered} \frac{52\cdot3^{(y+1)/(5)}}{52\cdot3^{(y)/(5)}} \\ =3^{(1)/(5)} \end{gathered}`

Thus, the above expression gives the requried value of factor.