Question

The hourly wage of some automobile plan workers went from $7.50 to $12.22 in 10 years (annual raises).If their wages are growing exponentially what will be their hourly wage in 10 more years?(nearest $0.10)

Answer 1

Define the exponential function

`A(t)=A_0e^(rt)`

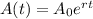
where A is the hourly wage.

Given that A(0) = 7.50 and A(10) = 12.22.

By using definition of A(t),

`\begin{gathered} 7.50=A_0e^0 \\ A_0=7.50 \end{gathered}`

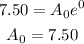
Then

`A(t)=7.5e^(rt)`

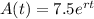
Now, use A(10)=12.22.

`\begin{gathered} 7.5e^(10r)=12.22 \\ e^(10r)=1.629 \end{gathered}`

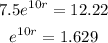
Take logarithm on both sides.

`\begin{gathered} 10r=\ln (1.629) \\ =0.488 \\ r=0.0488 \end{gathered}`

Substitute the value of r in A(t).

`A(t)=7.5e^(0.0488t)`

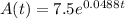
Find the wage after 10 more years.

Take t = 20 and substitute into A(t).

`\begin{gathered} A(20)=7.5e^(0.0488\cdot20) \\ =19.904 \end{gathered}`

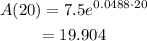
In 20 years, the daily wage will be $19.904.