Question

For the diagram below, if all three quadrilaterals are congruent, and if < A = 3x + 4 degrees and < G = x - 6 degrees, find x.

Answer 1

x = -5

Explanation:

We are told that all three quadrilaterals are congruent. This means that all three quadrilaterals are exact copies of each other.

Now let us compare quadrilaterals EFGH and CBAD. Angle A is quadrilateral to CBAD as angle G is to quadrilateral EFGH. Therefore,

`\angle G=\angle A`

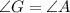
Now since,

`\begin{gathered} ∠G=x-6 \\ ∠A=3x+4 \end{gathered}`

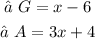
Therefore,

`\begin{gathered} ∠G=∠A \\ \Rightarrow x-6=3x+4 \end{gathered}`

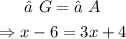
Now we just have to solve the above equation for x.

Adding 6 to both sides gives

`\begin{gathered} x-6+6=3x+4+6 \\ \Rightarrow x=3x+10 \end{gathered}`

subtracting 3x from both sides gives

`x-3x=3x+10-3x`
`-2x=10`

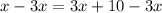
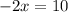
Finally, dividing both sides by -2 gives

`x=-(10)/(2)`
`\boxed{x=-5.}`

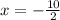
which is our answer!