Question

I am going to attach a picture of the question my teacher has already answered them and she wants me to show how she got the answer. I need the answer fast this is due in an hour

Answer 1

We can divide the prism in 3 pairs of equal rectangles as follows:

for the first pair, the area of one rectangle is

`\begin{gathered} A_1=\text{base}* height \\ A_1=7*21=147 \end{gathered}`

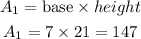
for the second pair, the area of one rectangle is

`\begin{gathered} A_2=\text{base}* height \\ A_2=16*7=112 \end{gathered}`

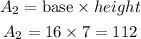
and finally, for the third pair, the area of one rectangle is

`\begin{gathered} A_3=\text{base}* height \\ A_3=16*21 \\ A_3=336 \end{gathered}`

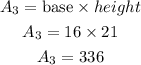
Therefore, the surface area S is given by

`S=2\cdot A_1+2\cdot A_2+2\cdot A_3`

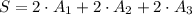
which leads to

`\begin{gathered} S=2\cdot147+2\cdot112+2\cdot336 \\ S=1190cm^2 \end{gathered}`

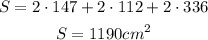
which corresponds to option C.