Question

Use the equation of the polynomial function f(x)=−2x3−x to complete the following.(a) State the degree and the leading coefficient.(b) Describe the end behavior of the graph of the function.(c) Support your answer by graphing the function.

Answer 1

The function given is,

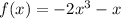
`f(x)=-2x^3-x`(a)

We need to find the degree and leading coefficient of the function.

The degree is the highest power of the polynomial.

We can see that it is a cubic polynomial, or, a third degree function.

The leading coefficient is the coefficient of the highest degree term.

In our case, -2 is the leading coefficient because it is the coefficient of x^3.

(b)

The end behavior of a polynomial function is the behavior of the graph of f(x) as x approaches positive infinity or negative infinity.

Let's graph the function:

From the graph, we can see,

• As x approaches infinity, the function approaches negative infinity

,

• As x approaches negative infinity, the function approaches positive infinity

This describes the end behavior of the function.

(c)

From our function graphed above, we see that "D", from the answer choices, represents the correct graph of this function.

Answer(s)(a)

The degree of the polynomial is 3 and the leading coefficient is - 2.

(b)

The curve opens down to the right because the leading coefficient is negative. Because the polynomial is cubic, the graph has end behaviors in the opposite direction, so the other end opens up to the left.

(c)

D