Question

A 250 g sticky hockey puck slides along a frictionless, horizontal ice surface at 75 m/s in the +x direction. It collides with a 500 g sticky puck originally sliding at 25 m/s in the -y direction. They collide perfectly inelastically. How much kinetic energy is lost in this collision?

Answer 1

Given data

*The given mass of the hockey puck is m = 250 g

*The puck moves at a speed is v_1 = 75 m/s

*The other given mass of the second puck is M = 500 g

*The second puck is moving at a speed in the -y-direction is v_2 = 25 m/s

Objects stick together after perfectly inelastic collision.

The x-component of the final velocity of the first puck is calculated as

`\begin{gathered} mv_1=(m+M)v_x \\ v_x=(mv_1)/((m+M)) \\ =((250)(75))/((250+500)) \\ =25\text{ m/s} \end{gathered}`

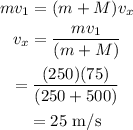
Similarly, the 'y-component' of the final velocity of the second puck is calculated as

`\begin{gathered} Mv_2=(m+M)v_y \\ v_y=(Mv_2)/((m+M)) \\ =16.67\text{ m/s} \end{gathered}`

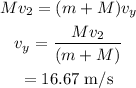
The formula for the magnitude of the velocity of both the pucks is calculated as

`\begin{gathered} v=\sqrt[]{v^2_x+v^2_y} \\ =\sqrt[]{(25)^2+(16.67)^2} \\ =30.04\text{ m/s} \end{gathered}`

The kinetic energy lost in the collision is calculated as