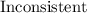Write both equations in standard form:
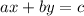
The first one is already written in standard form:
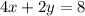
To write the second one in standard form, add 2x to both members of the equation:
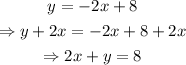
Notice that if we divide both members of the first equation by 2, we get:
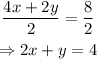
Then, the system of equations is equivalent to:
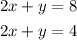
For the transitive property of equality, since both left members are the same, we can conclude from that system of equations that 8=4, which is false. Then, the system is inconsistent, since it leads to a contradiction.
Therefore, the answer is: