We know that each time the ball bounces it travels a distance of 3/4 the original height, that means that for each bounce the ball will rise:
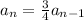
where a_n is the height of the nth bounce and a_(n-1) is the bounce n-1 (the previous one).
Now, from this formula we know that:
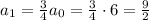
Therefore the explicit formula for the height of the nth bounce is:
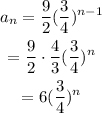
Then:
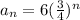
Now, to find the total distance it travels by the fifth bounce we follow:
The first time the ball hits the ground it has traveled a distance of 6 ft.
Now, for the second bounce we have:

(one distance up and one distance down).
For the third bounce we have:
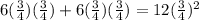
If we continue this process we notice that the ball will travel a total distance of:

but this can be written (for an infinity number of bounces) as:
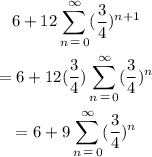
As we said this is for an infinity of bounces if we like only five bounces then we have:
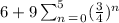
Now to find the distance in this case we do the sum and we get appoximately 35.5928 feet.