Question

how many liters of paint must you buy to paint the walls of a rectangular prism shaped room that is 20m x 15m, with a ceiling height of 8m.. if 1 Liter of paint covers 40m^2? the amount of paint needed is ____ liters. (Round up to the nearest integer as needed)

Answer 1

Answer: 14

Explanation:

Answer 2

For this question, we compute the superficial area of a rectangular prism without including the ceiling area nor the floor area. We will use the following formula:

`A=\text{ }(\text{rectangle perimeter)}\cdot\text{ height}`

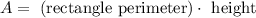
The rectangle perimeter is 2*(20m+15m)=70m. Substituting in the equation above we get:

`A=\text{ 70m}\cdot8m=560m^2`

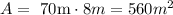
Therefore, the amount of paint needed is

`(560)/(40)\text{liters}=14\text{liters}`

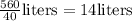
Answer: 14 liters.