Solution:
Given data:
Let the width of the box be
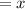
The volume of the box is
![V_{\text{box}}=400\operatorname{cm}]()
The height of the box is
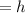
Let the length of the box be
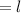
The length is four times the width of the base, this can be represented below as
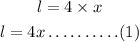
Part A:
Show that the height h of the box is given by

Concept:
To show that the height is given as above, we will use the volume of the box which is given below as
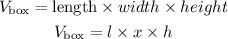
By substituting the values, we will have

Part B:
Show that the total surface area A of the box is given by
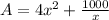
Concept:
To prove the above relation, we will use the formula of the area of the box below
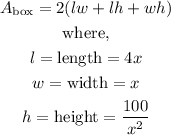
By substituting the values, we will have
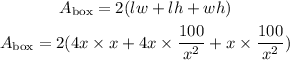
By simplifying the relation above, we will have
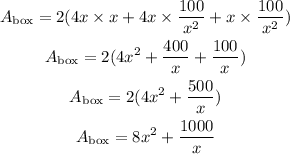
Hence,
The Total surface area of the box will be given below as
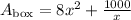
To determine the value of x which optimizes the total surface area of the box, and show
that it minimizes the total surface area, we will have to look for the first derivative of the function above
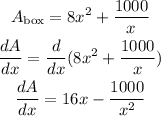
To find the value of x, we will substitute the value of dA/dx to be = 0
![\begin{gathered} (dA)/(dx)=0 \\ 16x-(1000)/(x^2)=0 \\ 16x=(1000)/(x^2) \\ (16x^3)/(16)=(1000)/(16) \\ x^3=62.5 \\ x=\sqrt[3]{62.5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6s52jox8gwime0b7h8menfchdeinkh7ar5.png)
To show the minimum value of x, we will have to look for the second derivative
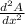
![undefined]()