Question

MN is parallel to XZMN is 6 units. Find the lengths of NZ and XZ.

Answer 1

Since these triangles are similar, we can express the ratios of their sides like this:

`(YX)/(YM)=(YZ)/(YN)=(XZ)/(NM)`

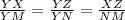
By taking the first two ratios replacing the known values and then solving for YZ, we get:

`\begin{gathered} (YX)/(YM)=(YZ)/(YN) \\ (YZ)/(3)=(10)/(5) \\ (YZ)/(3)=2 \\ YZ=2*3=6 \end{gathered}`

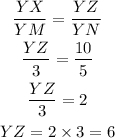
The length of NZ is the length of YZ minus the length of YN:

NZ=YZ-YN=6-3=3

Then, NZ equals 3

By taking the last two ratios we can calculate XZ, like this:

`\begin{gathered} (YZ)/(YN)=(XZ)/(NM) \\ (6)/(3)=(XZ)/(6) \\ (XZ)/(6)=(6)/(3) \\ (XZ)/(6)=2 \\ XZ=2*6 \\ XZ=12 \end{gathered}`

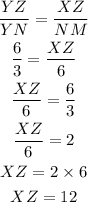
Then, XZ equals 12