Given the following equation:
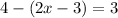
You can solve for "x" by following these steps:
1. You must distribute the negative sign of the left side of the equation:
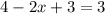
2. Now you need to add the like terms of the left side of the equation:
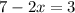
3. Apply the Subtraction property of equality by subtracting 7 from both sides of the equation:
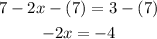
4. Finally, you can apply the Division property of equality by dividing both sides of the equation by -2:
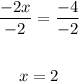
The answer is:
