Given that the mass of each ball is m = 6.8 kg
The distance between them is d = 2r
Here, r is the radius of the ball.
The gravitational force of attraction is
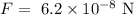
We have to find the radius of the ball.
The gravitational force formula is
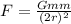
Here, the universal gravitational constant is
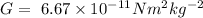
The radius will be
![\begin{gathered} r=\sqrt[]{(Gmm)/(4F)} \\ =\sqrt[]{(6.67*10^(-11)*6.8*6.8)/(4*6.2*10^(-8))} \\ =\text{ 0.114 m} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/5i4m3a3pd5vfyu6d7j44vnjrx931t0198d.png)
Thus, the radius of one of these balls is 0.114 m