Question

Match each equation with its solution set.2(5 – 4x) = 8x + 2a. no solution8(x + 5) = 8x + 40b. all real numbers2(5 – 4x) = 2 – 8xc. 1/28(x + 5) = 8x + 5d. 2

Answer 1

To match the equation with its solution set we need to solve each of them. Let's do that

First equation:

`\begin{gathered} 2(5-4x)=8x+2 \\ 10-8x=8x+2 \\ 8x+8x=10-2 \\ 16x=8 \\ x=(8)/(16) \\ x=(1)/(2) \end{gathered}`

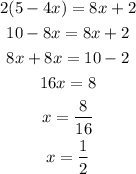
Second equation:

`\begin{gathered} 8(x+5)=8x+40 \\ 8x+40=8x+40 \end{gathered}`

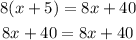
Since both sides of the equation are exactly the same expression we conclude that this equation is satisfied by all real numbers.

Third equation:

`\begin{gathered} 2(5-4x)=2-8x \\ 10-8x=2-8x \\ 8x-8x=2-10 \\ 0=-8 \end{gathered}`

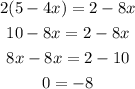
Since the last line is a contradiction we conclude that this equation has no solutions.

Fourth equation:

`\begin{gathered} 8(x+5)=8x+5 \\ 8x+40=8x+5 \\ 8x-8x=5-40 \\ 0=-35 \end{gathered}`

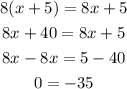
Once again we have a contradiction in the last line, then this equation has no solutions.

Then the correct match is:

First equation with c.

Second equation with b.

Third equation with a.

Fourth equation with a.