Question

Disturbed by speeding cars outside his workplace, Nobel laureate Arthur Holly Compton designed a speed bump (called the "Holly hump") and had it installed. Suppose a 1800-kg car passes over a hump in a roadway that follows the arc of a circle of radius 21.4 m as in the figure below.(a) If the car travels at 26.6 km/h what force does the road exert on the car as the car passes the highest point of the hump?(b) What is the maximum speed the car can have without losing contact with the road as it passes this highest point?

Answer 1

`\begin{gathered} (a)13,046N \\ (b)14.5m\/s\text{ or }52.2km\/h \end{gathered}`

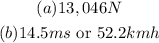
Step-by-step explanation

Parameters given:

Mass of the car, m = 1800 kg

Radius of arc, r = 21.4 m

(a) First, let us make a free body sketch of the problem:

where N = force exerted by the road on the car

W = weight of the car

v = velocity of the car

First, let us convert the given velocity to meters per second:

`\begin{gathered} v=26.6\cdot(1000)/(3600) \\ v=7.39m\/s \end{gathered}`

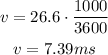
The centripetal force acting on the car as it moves in the semi-circular arc is given by:

`F=(mv^2)/(r)`

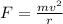
The total forces acting on the car is:

`N-W+F=0`

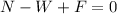
This implies that:

`\begin{gathered} N=W-F \\ N=mg-(mv^2)/(r) \\ N=(1800\cdot9.8)-(1800\cdot7.39^2)/(21.4)=17,640-4,593.54 \\ N=13,046N \end{gathered}`

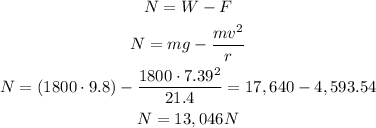
That is the force that the road exerts on the car.

(b) At the maximum speed, the car will start to lose contact with the road at N = 0:

`\begin{gathered} \Rightarrow0=W-F \\ 0=mg-(mv^2_m)/(r) \\ \Rightarrow(mv^2_m)/(r)=mg \\ \Rightarrow v^2_m=gr \\ \Rightarrow v_m=\sqrt[]{gr} \end{gathered}`

Substitute the values of g and r to solve for maximum speed, vm:

`\begin{gathered} v_m=\sqrt[]{9.80\cdot21.4} \\ v_m=\sqrt[]{209.72} \\ v_m=14.5m\/s \end{gathered}`

In km/h, that is:

`\begin{gathered} 14.5\cdot(3600)/(1000) \\ 52.2km\/h \end{gathered}`

That is the maximum speed that the car can have.