GIVEN
Two triangles ABC and ACD where two corresponding sides of the two triangles are equal.
SOLUTION
The two triangles have equal sides such that:
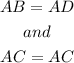
By this, the length of the remaining sides BC and DC are related such that the side opposite the greater angle has the greater length.
Since
 Substitute known values into the inequality:
Substitute known values into the inequality:
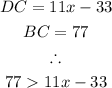
Solving the inequality:

Recall that the side DC has to be greater than 0. Therefore:
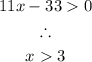
Combining both solutions:
[tex]3
ANSWER