Question

55 mL of alcohol (density = 0.75g/mL) is mixed with 25 g of water (density = 1.00 g/mL). Whatis the density of the mixture?

Answer 1

Given:

The volume of alcohol, V_a=55 mL

The density of the alcohol, ρ_a=0.75 g/mL

The mass of the water in the mixture, M_w=25 g

The density of water, ρ_w=1.00 g/mL

To find:

The density of the mixture.

Step-by-step explanation:

The mass of the alcohol in the mixture is given by,

`\begin{gathered} M_a=V_a\rho_a \\ =55*0.75 \\ =41.25\text{ g} \end{gathered}`

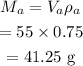
The volume of the water in the mixture,

`V_w=(m_w)/(\rho_w)`

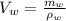
On substituting the known values,

`\begin{gathered} V_w=(25)/(1.00) \\ =25\text{ mL} \end{gathered}`

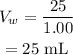
Thus the density of the mixture is given by,

`\begin{gathered} \rho_=\frac{total\text{ }mass}{total\text{ }volume} \\ =(m_a+m_w)/(V_a+V_w) \end{gathered}`

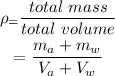
On substituting the known values,

`\begin{gathered} \rho=(41.25+25)/(55+25) \\ =0.83\text{ g/mL} \end{gathered}`

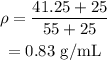
Final answer:

Thus the density of the mixture is 0.83 g/mL