Question

while test flying the new f-22 raptor fighter jet, test pilot bob put the plane in a horizontal loop while flying at the speed of sound (343 m/s). what is the minimum radius that the plane can fly if bobs centripetal acceleration cannot exceed 5g (5 times the acceleration due to gravity)?

Answer 1

Given

v = 343 m/s

ac = 5g

ac = 5*9.8 m/s^2

ac = 49 m/s^2

where,

v: velocity

ac = centripetal aceleration

Procedure

We call the acceleration of an object moving in uniform circular motion—resulting from a net external force—the centripetal acceleration ac; centripetal means “toward the center” or “center seeking”.

Formula

`\begin{gathered} a_c=(v^2)/(r) \\ r=(v^2)/(a_c) \\ r=((343m/s)^2)/(49m/s^2) \\ r=2401\text{ m} \end{gathered}`

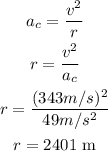
The minimum radius not to exceed the centripetal acceleration is 2401 m.