SOLUTION
(a) The probability of at least 4 girls means the probability of getting 4 girls or the probability of getting 5 girls.
Using binomial probability formula

Where p is the probability of success,
q = probability of failure
n = number of outcomes
x = number of successful events.
Probability of getting 4 girls means 4 success (4 girls) and 1 failure (1 boy)
So,
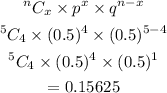
Probability of getting 5 girls means all 5 success (5 girls) and 0 failure (0 boy)
So, we have
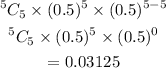
So, The probability of at least 4 girls becomes
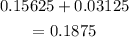
Therefore, the answer is 0.1875
(b) Probability of at most 4 girls is 1 - the probability of 5 girls
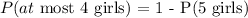
P(5 girls) = 0.03125
So
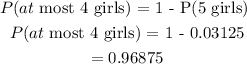
Therefore, the answer is 0.9688 to four decimal places