The Solution:
From the given graph, we have that the two complex numbers have only real parts. This means that:
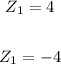
We are required to plot the graph of
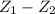
So,

To plot the required graph, we shall locate point +8 on the real line as mark in red color in the attached graph below: