Answer
The amount that would have decayed after exactly 5 half-lives is 96.875 mg
Step-by-step explanation
Given:
Half-life of the substance, = 471.7 days
Initial quantity of the substance = 100.0 mg
Number of half-life, n = 5
What to find:
The milligrams of the sample that would have decayed after exactly 5 half-lives.
Solution
Note that the length of the half-life played no role in this calculation.
The first step is to calculate the amount of the 100.0 mg sample remaining after 5 half-lives using the half-life formula.
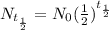
So the amount remaining after exactly 5 half-lives is

The amount that would have decayed = Initial amount - Amount remaining after exactly 5 half-lives.
The amount that would have decayed = 100.0 mg - 3.125 mg = 96.875 mg
Therefore, The amount that would have decayed after exactly 5 half-lives is 96.875 mg