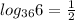Step-by-step explanation:
Given;
We are given the following equation;
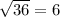
Required;
We are now required to write this as a Logarithmic equation.
Step-by-step solution;
To do this, we would first take the left side of the equation and simplify the radical;
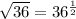
We now re-write the equation as shown below;
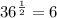
Now we can apply the log rule which is;
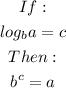
For example;
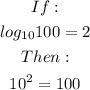
Therefore we would now have;
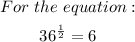
ANSWER: